7.5 Penambah BCD
7.5 Penambah BCD
Penjumlah BCD digunakan untuk melakukan penjumlahan bilangan BCD. Digit BCD dapat memiliki salah satu dari sepuluh kemungkinan representasi biner empat bit, yaitu, 0000, 0001,...., 1001, ekuivalen dengan bilangan desimal 0, 1,..., 9. Ketika kita mulai menjumlahkan dua digit BCD dan kita asumsikan ada input carry juga, bilangan biner tertinggi yang bisa kita dapatkan adalah setara dengan angka desimal 19 (9 + 9 + 1).
 |
| gambar 7.20 |
Bilangan biner ini akan menjadi (10011)2. Sebaliknya, jika kita melakukan penjumlahan BCD, kita harapkan jawabannya adalah (0001 1001)BCD. Dan jika kita membatasi bit keluaran ke minimum yang diperlukan, jawabannya dalam BCD adalah (1 1001)BCD. Tabel 7.1 mencantumkan hasil yang mungkin dalam biner dan hasil yang diharapkan dalam BCD ketika kita menggunakan penambah biner empat bit untuk melakukan penjumlahan dua digit BCD. Jelas dari tabel bahwa, selama jumlah dua digit BCD tetap sama dengan atau kurang dari 9, penambah empat bit menghasilkan output BCD yang benar.
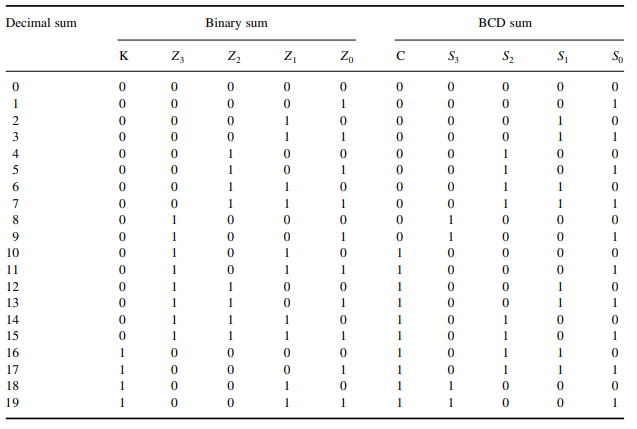 |
| Tabel 7.1 Hasil dalam biner dan hasil yang diharapkan dalam BCD menggunakan penambah biner empat bit untuk melakukan penjumlahan dua digit BCD |
Jumlah biner dan jumlah BCD dalam hal ini adalah sama. Hanya jika jumlahnya lebih besar dari 9 maka kedua hasil tersebut berbeda. Dapat juga dilihat dari tabel bahwa, untuk jumlah desimal lebih besar dari 9 (atau jumlah biner yang setara lebih besar dari 1001), jika kita menambahkan 0110 ke jumlah biner, kita bisa mendapatkan jumlah BCD yang benar dan output carry yang diinginkan juga . Ekspresi Boolean yang dapat menerapkan koreksi yang diperlukan ditulis sebagai
C = K +Z3.Z2 +Z3.Z1 (7.17)
Persamaan (7.17) menyiratkan sebagai berikut. Koreksi perlu diterapkan setiap kali K = 1. Ini menangani empat entri terakhir. Juga, koreksi perlu diterapkan setiap kali Z3 dan Z2 adalah '1'. Ini menangani empat entri berikutnya dari bawah, yang sesuai dengan jumlah desimal yang sama dengan 12, 13, 14 dan 15. Untuk dua entri yang tersisa yang sesuai dengan jumlah desimal yang sama dengan 10 dan 11, koreksi diterapkan untuk kedua Z3 dan Z1, menjadi '1'. Saat mengimplementasikan perangkat keras, 0110 dapat ditambahkan ke output jumlah biner dengan bantuan penambah biner empat bit kedua. Logika koreksi seperti yang ditentukan oleh ekspresi Boolean (7.17) harus memastikan bahwa (0110) ditambahkan hanya ketika ekspresi di atas terpenuhi. Jika tidak, jumlah keluaran dari penambah biner pertama harus diteruskan seperti itu ke keluaran akhir, yang dapat dicapai dengan menambahkan (0000) pada penambah kedua. Gambar 7.21 menunjukkan susunan logika penambah BCD yang mampu menjumlahkan dua digit BCD dengan bantuan dua penambah biner empat bit dan beberapa logika kombinasional tambahan.
Penjumlah BCD yang dijelaskan dalam paragraf sebelumnya hanya dapat digunakan untuk menjumlahkan dua angka BCD satu digit. Namun, susunan kaskade perangkat keras penambah BCD satu digit dapat digunakan untuk melakukan penambahan nomor BCD beberapa digit. Misalnya, penambah BCD n-digit akan membutuhkan n tahapan seperti itu dalam kaskade. Sebagai ilustrasi, Gambar 7.22 menunjukkan diagram blok rangkaian penjumlahan dua bilangan BCD tiga angka. Penjumlah BCD pertama, berlabel LSD (Least Significant Digit), menangani digit BCD paling tidak signifikan. Ini menghasilkan output jumlah (S3 S2 S1 S0), yang merupakan kode BCD untuk digit paling signifikan dari jumlah. Ini juga menghasilkan pembawa keluaran yang diumpankan sebagai pembawa masukan ke penambah BCD berikutnya yang lebih tinggi. Penjumlah BCD ini menghasilkan keluaran penjumlahan (S7 S6 S5 S4), yang merupakan kode BCD untuk digit kedua dari penjumlahan, dan keluaran carry. Keluaran carry ini berfungsi sebagai carry masukan untuk penambah BCD yang mewakili digit paling signifikan. jumlah output (S11 S10 S9 S8) mewakili kode BCD untuk MSD jumlah.
 |
| gambar 7.21 Penjumlah BCD satu digit. |
 |
| Gambar 7.22 |
Contoh 7.1
Untuk rangkaian setengah penambah pada Gambar 7.23(a), input yang diterapkan pada A dan B adalah seperti yang ditunjukkan pada Gambar 7.23(b). Plot output SUM dan CARRY yang sesuai pada skala yang sama.
Solusi
Bentuk gelombang SUM dan CARRY dapat diplot dari pengetahuan kita tentang tabel kebenaran setengah penambah. Yang perlu kita ingat untuk menyelesaikan masalah ini adalah 0+0 menghasilkan '0' sebagai output SUM dan '0' sebagai CARRY. 0 +1 atau 1+0 menghasilkan '1' sebagai output SUM dan '0' sebagai CARRY. 1 +1 menghasilkan '0' sebagai output SUM dan '1' sebagai CARRY. Bentuk gelombang keluaran seperti ditunjukkan pada Gambar 7.24.
 |
| gambar 7.23 Contoh 7.1 |
 |
| gambar 7.24 Solusi dari contoh 7.1 |
Contoh 7.2
Mengingat ekspresi Boolean yang relevan untuk rangkaian setengah-penambah dan setengah-pengurang, rancang rangkaian setengah-penambah-pengurang yang dapat digunakan untuk melakukan penjumlahan atau pengurangan pada dua bilangan satu bit. Operasi aritmatika yang diinginkan harus dapat dipilih dari input kontrol.
Solusi
Ekspresi Boolean untuk setengah-penambah dan setengah-pengurang diberikan sebagai berikut:
Setengah penambah
Jika kita menggunakan inverter terkontrol untuk melengkapi A dalam kasus rangkaian setengah-pengurang, maka perangkat keras yang sama juga dapat digunakan untuk menambahkan dua angka satu bit. Gambar 7.25 menunjukkan diagram rangkaian logika. Ketika input kontrol adalah '0', variabel input A dilewatkan tanpa pelengkap ke input gerbang NAND. Dalam hal ini, gerbang AND menghasilkan keluaran CARRY dari operasi penjumlahan. Gerbang EX-OR menghasilkan keluaran SUM. Di sisi lain, ketika input kontrol adalah '1', gerbang AND menghasilkan output BORROW dan gerbang EX-OR menghasilkan output DIFFERENCE. Jadi, '0' pada input kontrol menjadikannya setengah penambah, sedangkan '1' pada input kontrol menjadikannya setengah pengurang.
Setengah pengurangan



Comments
Post a Comment